

Seminararbeit zum interdisziplinären Seminar "Natürliche und künstliche Intelligenz" ETHZ / UNIZH
1. Einführung: Der psychologische Raum
2. Visualisierung von Category-Learning
3 Visualisierung des Lern-Prozesses
4 Komplexität von Kategorien-Lern-Situationen
Anhang A - Die Software "Mind Geometry"
Anhang B - Input-File Spezifikationen
 |
 |
 |
Der "Psychologische Raum" ist ein Modell für den Input, den die menschliche oder künstliche Wahrnehmung erhält. Es wird davon ausgegangen, dass man jeden Stimulus als Punkt in einem n-dimensionalen Raum auffassen kann.
ZB. bilden die Dimensionen Grösse, Farbe, Form etc. einen psychologischen Raum.
Ein psychologischer Raum beim Erkennen von ein paar geometrischen Formen (vgl. Abb. 1) könnte beispielsweise so vereinfacht werden:
Dimensionen:
- Farbe (Blau / Gold)
- Form (Fuss / Stern)
- Grösse

Abb.1: Beispiel einer Stimulus-Menge zu einem 3-dimensionalen psychologischen Raum
Alle Stimuli sind eindeutig durch einen Punkt im psychologischen Raum veranschaulicht. Sie können dem Kategorisierungsmodell (Mensch oder Maschine) als Input in der Form eines Vektors präsentiert werden, zB.:
(Farbe: Gold , Form: Fuss, Grösse: gross)

Psychologische Dimensionen können sowohl diskret (zB. Form: Fuss oder Stern) als auch kontinuierlich (zB. Grösse) sein.
Ähnlichkeit von zwei Objekten wird als Distanz im psychologischen Raum angesehen. Als Metrik wird dabei meistens die gewöhnliche Distanz (euklidische Metrik) oder City-Block (Summe der Distanzen in Richtung der Koordinatenachsen) verwendet.
![]()
![]()
Wenn k die Anzahl Kategorien ist, dann ist der Zustand eines Kategorien-Lern-Systems (Mensch oder Maschine) durch ein k-dimensionales Feld über dem n-dimensionalen psychologischen Raum eindeutig bestimmt. Dh. der Zustand ist bestimmt, wenn jedem Punkt des psychologischen Raumes zugeordnet ist, wie stark ihn das Kategorisierungsmodell mit jeder Kategorie assoziiert.
Das Hauptproblem bei der Visualisierung ist nun, diesen Zustand nun auf 2 oder 3 Dimensionen zu darzustellen, ohne die wichtigen Informationen zu verlieren.
Wenn man dem Psychologischen Raum der Dimension n eine diskrete Dimension "Kategorie" hinzufügt, dann kann man den Zustand des Systems als (eindimensionales) Skalarfeld über diesem neuen Raum auffassen. Der Skalar bedeutet dann, wie stark die Bindung an der Stelle im psychologischen Raum mit der Kategorie an dieser Stelle ist.
Das Problem der Visualisierung ist damit reduziert auf die Visualisierung von k Skalarfeldern über dem psychologischen Raum.
Im folgenden wird ganz kurz auf die wichtigsten Lösungsstrategien zu diesem Problem eingegangen, die schlussendlich zum Programm "Mind Geometry" geführt haben.
Um Skalarfelder über mehr als 2-dimensionalen Räumen zu visualisieren, gibt es im wesentlichen 2 Möglichkeiten:
a) Visualisierung von Aequipotentialflächen
Visualisierung der Potentialflächen eines Skalarfeldes bedeutet Zeichnen der scharf abbegrenzten Teilgebiete, in denen der Wert des Feldes unter einen gegebenen Wert sinkt. Die Körper werden dabei mit Rendering- oder Raytracing-Methoden dargestellt. Dies ist die am meisten verbreitete Methode in der Rechnergestützten Visualisierung. Der Nachteil dabei ist, dass die innere Struktur der Gebiete unsichtbar bleibt. Die quantitative Information innerhalb und ausserhalb der Teilgebiete geht grösstenteils verloren.
b) Transparente Methoden ("Volume Rendering")
Um auch die innere und quantitative Struktur des Skalarfeldes wiederzugeben muss eine Visualisierungsmethode Transparenz zulassen. Eine mögliche Realisierung einer transparenten Projektion ist, den Raum senkrecht zur Projektionsrichtung in möglichst dünne Schichten zu schneiden. Wenn die Werte in diesen Schichten durch Skalarwerte dargestellt werden, dann kann man alle Schichten transparent zusammenrechnen, und erhält die Projektion auf eine Schicht; zB. die Betrachtungsebene. Das Verrechnen von mehreren Schichten geschieht zum Beispiel durch Multiplikation der Transparenz-Werte. Dh. wenn ai der Wert auf der Schicht i ist (und zwischen 0 und 1) und s die Anzahl Schichten, dann gilt
![]()
Diese Projektion ist also voll kommutativ. Daraus wird klar, dass die Transparenz und damit der Informationsverlust gleichmässig ist. "Mind Geomerty" benützt deshalb diese Darstellungsart. Ungleichmässiger Informationsverlust wie zB. bei traditionellem Rendering wäre bei der Darstellung des psychologischen Raumes hinderlich.
Um Objekte im n-dimensionalen Raum zu visualisieren, wird die beschriebene Projektion einfach n-3 bzw. n-2 mal angewendet. dh. man projiziert auf den Raum eine Dimension tiefer, bis man schlussendlich im Dreidimensionalen bzw auf der Betrachtungsebene angelangt ist. Wenn viele Projektionen nacheinander angewandt werden wird es für den Betrachter sehr schwierig, das Feld richtig zu interpretieren. Auch hier ist es deshalb von Vorteil für die Anschaulichkeit und Kontrolle, wenn Transparenz zugelassen wird.
Ein wichtiges Postulat von Kruschke ist, dass das Kategorien-Lernen von Fehlern gesteuert wird (Error Driven Learning). Das Sprichwort "Aus Fehlern lernt man" hat auch seine Bedeutung bei der Kategorisierung.
Im folgenden werden die entwickelten Methoden verwendent, um "Error Driven Learning" bei Kruschkes künstlichen Kategorisierungssystem ALCOVE (1992) zu visualisieren.
[ Eine sehr gute und verständliche Einführung zu ALCOVE findet man im Paper von Serge Trefzger und Rolf Hintermann ]
Die Visualisierungssoftware zeigt klar, was "Error Driven Learning" bei ALCOVE bedeutet; Da das System bei jedem Fehler seine Parameter wieder anpasst, läuft der Lernprozess stark oszillierend ab. Die Visualisierung zeigt sehr schön, wie diese Oszillation bei den ersten Lernschritten sehr stark ist, und dann mit dem Lernfortschritt immer kleiner wird. Mit dem optimalen Lernen scheint die geometrische Form gegen die "richtige", optimale Form zu konvergieren.
Eine wichtige Eigenschaft von Kategorisierungsmodellen ist das Lernen dimensionaler Relevanz. Damit ist gemeint, dass ein System unbedingt herausfinden muss, welchen Input-Dimensionen die grösste Beachtung geschenkt werden muss, bzw. welche Dimensionen für die Kategorisierung eher unwichtig sind. Kruschke spricht von "Attention learning" als wichtiger Voraussetzung für ein Modell des menschlichen Lernens.
Das ALCOVE-Modell benutzt für jede Input-Dimension ein einfaches Gewicht, um die Wichtigkeit der Dimension zu definieren. Falls nun eine Dimension für die Kategorisierung irrelevant wird, so wird sie immer weniger stark gewichtet und verschwindet schliesslich ganz. Das geometrische Objekt im psychologischen Raum wird dadurch unscharf in der entsprechenden Richtung.

Abb.2: Beispiel einer Figur, die nur noch eine Struktur in einer Dimension hat
Dass ALCOVE nur ein einfaches Gewicht besitzt um die Relevanz der Dimensionen zu definieren, erweist sich als grosser Nachteil dieses Systems. Modernere Modelle für die menschliche Kategorisierung können ihre Empfindlichkeiten ("attention strengths") viel differenzierter einstellen und anpassen. Das neuere System SUSTAIN (Supervised and Unsupervised STratified Adaptive Incremental Network) von Love & Medin definiert beispielsweise für jeden Knoten ein eigenes Empfindlichkeitsfeld. Die Relevanz der Dimensionen kann also für jedes Teilproblem varieren. Die geometrischen Figuren zu einem SUSTAIN-Model können deshalb auch reichhaltiger und differenzierter werden als jene zu ALCOVE.
Es wäre sehr wichtig, ein möglichst exaktes Mass für die Schwierigkeit verschiedener Kategorisierungen zu finden. Da der Zustand eines Kategorien-Lernsystems durch k Skalarfeldern über dem psychologischen Raum beschrieben wird, scheint die Komplexität dieser geometrischen Figur in einem gewissen Sinn ein Mass für die Schwierigkeit zu sein.
Im folgenden Abschnitt wird nun versucht, damit Tests über die Schwierigkeit von verschiedenen Kategorisierungen (zB. Shepard) zu reproduzieren.
Shepard, Hovland, und Jenkins führten 1961 einen einfachen Versuch durch, um mehr über das menschliche Kategorisierungsverhalten zu erfahren. Sie wählten dazu einen psychologischen Raum mit 3 binären Input-Dimensionen wie zB.
- Farbe (Blau / Gold)
- Form (Fuss / Stern)
- Grösse (klein / Gross)

Abb.3: Acht mögliche Objekte für den Shepard-Test
Die 8 Objekte mussten nun in 2 Kategorien eingeordnet werden. Dabei gibt es 6 unterschiedbare Varianten, die beiden Kategorien (zu je 4 Objekten) zu bilden:

Abb.4: Die Kategorisierungen (psych. Raum mit 3 binären Input-Dimensionen)
Shepard interessierte nun, welche Kategorisierungen einfacher zu lernen waren, und welche schwieriger. Er untersuchte für jede Variante, wieviele Lernschritte es brauchte, bis die Probanden alle Objekte fehlerfrei in die richtige Kategorie einordnen konnten. Das Resultat war, dass Typ 1 mit Abstand am einfachsten zu lernen ist, und Typ 6 am schwierigsten. Die Ordnung der Typen nach Schwierigkeit ist 1<2<(3,4,5)<6 .
Die 6 Kategorisierungen, die Shepard verwendete sind natürlich sehr einfach, aber praktisch alle bisher bekannten künstlichen Kategorisierungsmodelle scheiterten an diesem Test, dh. produzierten ganz andere Reihenfolgen der Schwierigkeit. Diese Systeme schieden deshalb aus als Modell für das menschliche Kategorien-Lernen.
Die einzigen drei bekannten Modelle, die die Resultate von Shepard reproduzieren konnten, sind im Moment
ALCOVE (Attention Learning COVEring map) (Kruschke, 1992),
RULEX (Rule-plus-exception model) (Nosofsky, Palmeri, & McKinley, 1994) und
SUSTAIN (Supervised and Unsupervised STratified Adaptive Incremental Network) (Love & Medin 1998).
| Typ 1 quicktime movie  |
Typ 2 quicktime movie  |
Typ 3 quicktime movie  |
Typ 4 quicktime movie  |
Typ 5 quicktime movie  |
Typ 6 quicktime movie  |
Der Versuch, die Reihenfolge 1<2<(3,4,5)<6 zu erklären führte relativ lange zu keinen Resultaten. Erst Jacob Feldman (Artikel in Nature vom Oktober 2000), konnte die Reihenfolge mit der Komplexität von entsprehenden Logischen Formeln (Boolean-Ausdrücke) für die Kategoriezugehörigkeit erklären. Seine Argumente für die Komplexität der Formeln sind jedoch heuristischer Natur und stimmen bei komplexeren Situationen nicht mehr gut mit den wirklichen menschlichen Daten überein.
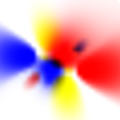
Das Visualisieren des Lernens der 6 Kategorisierungen (für die Simulation wurde ALCOVE verwendet) kann Shepards Reihenfolge in gewissem Sinn über die Komplexität der geometrischen Formen erklären. Die Geometrischen Objekte, die beim Lernen im psychologischen Raum "entstehen", werden im Programm laufend gedreht, um sie von allen Seiten betrachten zu können. Bei Shepard 1 ist die Drehung des Objekts auf den ersten Blick als Drehung um eine Achse zu erkennen. Das Objekt Shepard 6 hat eine etwas kompliziertere Form mit 2 x 3 "Beinen", und man kann die Drehung nur noch schwer nachvollziehen; Es wird schwierig, nur schon die Drehachse genau lokalisieren zu können.
Die Schwierigkeits-Hitliste bei der "Komplexität" der 6 Visualisierungen (Erkennen der Rotationen) stimmt mit Shepards Reihenfolge überein.
Zusammengefasst:
Die Komplexität der geometrischen Figur, die bei Category-Learning im psychologischen Raum "entsteht", scheint die Schwierigkeit der Kategorisierung zu definieren. Da die Figuren durch k Skalarfelder über einem n-dimensionalen Raum beschrieben werden, ist es relativ schwierig, ein exaktes Mass für die Komplexität der geometrischen Figuren zu finden. "Erkennbarkeit einer Rotation" könnte eine Annäherung in diese Richtung sein.
"Mind Geometry" ist ein Mac-Programm zur Realtime-Visualisierung von Category-Learning. Eingebaut ist bis jetzt nur eine ALCOVE-Implementation. "Mind Geometry" arbeitet mit einem gleichmässigen 3D-Gitter mit Kantenlängen zwischen 3 und 60 Punkten, dh. es sind bis zu 200'000 Gitterpunkte (Samples) im psychologischen Raum möglich.
Die Input-Files (Text-Dateien) enthalten alle Informationen und Trainings-Schritte für den Lern-Prozess und können einfach modifiziert werden (Siehe Anhang B)
|
Systemanforderungen: Mac PowerPC, MacOS 8 - 9.2.2, Farbbildschirm download(132kb sit-Datei, öffnet mit StuffIt-Expander) |
Der Quelltext von "Mind Geometry" (leider noch etwas chaotisch, in C für MPW).
2 // anzahl kategorien
8 // anzahl knoten
3 // anzahl dimensionen
255 0 0 // farbe der kategorie 1 (hier rot)
0 0 255 // " " " 2 (hier blau)
// die knoten-koordinaten aller knoten (für ALCOVE)
0 0 0
0 0 1
0 1 0
1 0 0
1 1 1
1 1 0
1 0 1
0 1 1
8 // anzahl lernschritte (exemplare)
// die einzelnen lern-exemplare mit kategorie
0 0 0 0
0 0 1 0
0 1 0 0
1 0 0 0
1 1 1 1
1 1 0 1
1 0 1 1
0 1 1 1
Feldman, J. (2000). Minimization of Boolean complexity in human concept learning. NATURE VOL 407, 5 OCTOBER 2000, Seite 630f
Kruschke, J. K. (1992). ALCOVE: An exemplar-based connectionist model of category learning. Psychological Review, 99, 22-44.
Love, B. & Medin, D. & Gureckis, T. (1998). SUSTAIN: A Network Model of Category Learning
Love, B. & Medin, D. (1998). Modeling Item and Category Learning
Dauger, D. (2001). Real-Time Visualization of the Quantum Mechanical Atomic Orbitals, dauger.com/orbitals
Jaggi, M. (2001). Visualizing Atom Orbitals in Real-Time, www.m8j.net/orbitals
Text, pictures, videos and software ©reated by Martin Jaggi 2002 m.jaggi@gmx.net